前面两节对二进制、八进制和十六进制进行了说明,接下来讲一下不同进制之间的数字是如何转换的,这在编程中经常会用到,尤其是C语言。
其他进制向十进制转换
二进制、八进制和十六进制向十进制转换都是非常容易的,就是“按权相加”。
所谓“权”,也即“位权”。例如,十进制第1位的位权为100=1,第2位的位权为101=10,第3位的位权为102=100;而二进制第1位的位权为20=1,第2位的位权为21=2,第3位的位权为22=4。设数字所采用的进制为N(基数也是N),那么第 i 位的位权为 N(i-1)。
不同进制转换为十进制举例:
- 二进制:1001 = 1×23 + 0×22 + 0×21 + 1×20 = 8 + 0 + 0 + 1 = 9
- 二进制:101.1001 = 1×22 + 0×21 + 1×20 + 1×2-1 + 0×2-2 + 0×2-3 + 1×2-4 = 4 + 0 + 1 + 0.5 + 0 + 0 + 0.0625 = 5.5625
- 八进制:0302 = 3×82 + 0×81 + 2×80 = 192 + 0 + 2 = 194
- 八进制:0302.46 = 3×82 + 0×81 + 2×80 + 4×8-1 + 6×8-2 = 192 + 0 + 2 + 0.5 + 0.09375= 194.59375
- 十六进制:0Xea7 = 14×162 + 10×161 + 7×160 = 3751
十进制转换为二进制——辗除法
上节的表格中给出了简单的十进制和二进制的转换关系,要想获得更多的转换关系,可以使用辗除法。辗除法也就是“除模取余”法。除模取余就是将一个几进制的数转化成另一个进制时, 另一个进制的基数就是模,用将要转化的进制数除以模,取它的余数。
下图以十进制的“19”转换为二进制为例进行讲解:
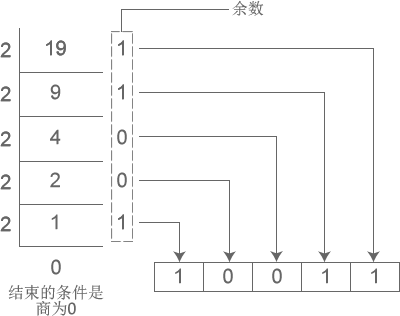
图1:19 转换为二进制
如图所示,以2为除数,一直相除下去,直到商为0,余数则为求得的二进制数。
注意:余数要倒序排列,也就是说,最先求得的余数排在二进制的最后面,最后求得的余数排在二进制的最前面。上面的例子中,最后求得的二进制数为 10011。
虽然其他进制也可以按照辗除法来转换,但是比较麻烦,下面介绍更简单的方法。
二进制和八进制的转换
二进制向八进制的转换是每三位二进制数转换为一位八进制数,运算的顺序是从低位向高位依次进行,高位不足三位用零补充。以二进制“1011101”为例,如下图所示:
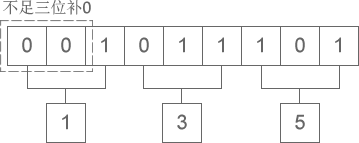
图2:二进制转八进制
转换的结果为:1011101 = 0135
八进制向二进制转换的思路是八进制的一位转换为二进制的三位,运算的顺序是从低位向高位依次进行。同样以八进制“0135”为例,如下图所示:
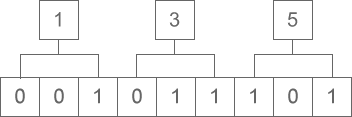
图3:八进制转二进制
转换的结果为:0135 = 1011101
二进制和十六进制的转换
二进制向十六进制转换时,四位转换成十六进制的一位,运算的顺序是从低位向高位依次进行,高位不足四位用零补。以“1110011”转换成十六进制为例,如下图所示:
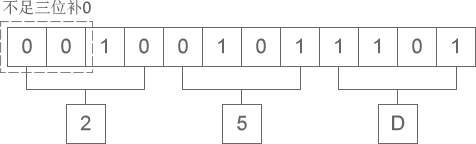
图4:二进制转十六进制
转换的结果为:1001011101 = 0X25D
十六进制向二进制转换,就是把十六进制的一位转换成二进制的四位,注意运算的顺序是从低位向高位依次进行。同样以十六进制“0X25D”为例,如下图所示:
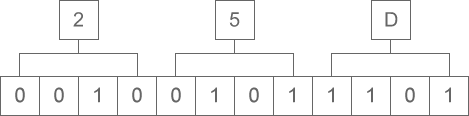
图5:十六进制转二进制