认知计算是将神经科学、超级计算、纳米技 术结合,用于发现、证明和传递大脑的核心算法。
什么是心智?目前,无论是科学家还是哲学家都还没有就其普遍的定义或解释达成共识。通俗地说,我们将心智理解为包括感觉、知觉、行动、情感和认知的一组过程。心智能把由视觉、听觉、触觉、味觉和嗅觉获取到的模糊信息集成起来;它能形成时空关联和抽象概念;它能够进行决策并产生复杂、协调的行动。
认知计算的目标是在心智能力的启发下,发展一种连贯、统一和普遍的计算机制。我们试图实现一种统一的心智计算理论,而不是简单地将按不同的认知过程和独立的解法单独构造出来的零碎解决方案拼凑在一起。人工智能领域的先驱者艾伦·纽威尔(Allen Newell)将这种计算理论描述为“针对所有认知行为的一组单一机制。我们的最终目标是一种关于人类认知的统一理论。”
历史上,很多彼此独立的领域曾采用完全不同的方法对类心智计算进行过探索,其中一部分我们在这里会有所提及。一方面,作为认知科学一个分支的人工通用智能(AGI)或者人工智能(AI) [10]采用系统级方法来合成类心智计算机。由于心智是由大脑湿件生成的,因此神经科学[18]采用组件级方法来理解心智是如何产生的。通过自上而下的分解简化方式,认知神经科学 [9]试图将理论认知科学与实验心理学、生物级神经科学进行结合。与之相反,系统神经科学 [18]则是通过自下而上的构造方式,对多个空间和时间范围的实验数据进行综合。这种多样化的研究方法反映了研究思路的多样性,由于心智—脑问题具有深远的技术重要性和极大科学难度,这种多样性是必要的。科学的发展繁荣就体现在多个群体拥有不同、互补、并行的观点,并且工作在不同的抽象层次上。
在这个背景下,我们所提出的全新的、充满前景的方法,是利用大规模计算机模拟来对大量的神经科学数据集进行操作。如今,将从神经生理学和神经解剖学领域精选出的研究成果结合,可以实现在小型哺乳动物大脑规模上的近实时模拟。虽然我们还只能报告十分初步的成果,但是我们的憧憬是远大的。我们始终不变的追求是发现、证明和传递大脑的核心算法,并获得对心智如何感知、思考和行动的深刻的科学解释。由此,将会产生全新的认知系统、计算体系结构、编程范式、实际应用和智能化商用机器。
理论基础
丘奇兰德(Churchland)和索诺斯基(Sejnowski)的表述将我们的理论依据恰当而充分地表述出来,他们指出:“如果不需要理解大脑自身本质就能够理解认知的本质,这将是一件很不错的事。但令人遗憾的是,在缺乏神经生物学约束的情况下,对这些问题进行有效的理论化即使并非完全不可能也是很困难的。其主要原因是计算的空间非常巨大,并且关于如何实现认知操作的问题能想到的解法有很多。神经生物学数据为计算理论提供了必要的约束条件,从而为缩小搜索空间提供了有效率的方法。同样重要的是,这些数据充分暗示了哪些是可能真实出现的,哪些是计算策略演化过程中可能碰巧发生。”
如今,神经科学拥有大量详细的生物学观察报告,正如坎德尔(Kandel)等所著的总共1 414页的现代入门教程《神经科学原理》中所反映的 [18]。作为神经科学学家,我们将这些观察报告看作是一个由对应认知生物学机理的线索所构成的网络。而作为工程师,我们会对这些报告有完全不同的认识。大脑是一个解决认知计算问题方法的典型例子,而神经科学的观察报告则是对于解决方法形式的部分约束条件。区分神经科学和认知计算就如同将小麦从谷壳中分离出来。
我们针对如何构建大脑的功能性模拟,对基本的神经学约束条件进行了探索,首先对从大脑的布线图获知的结构性制约进行了描述。其核心思想是大脑的神经网络是一个多尺度的稀疏有向图。特别是,局部、短距离的连接可以通过重复规范的子回路的统计变化来描述,而全局、远距离的连接则可以通过一个特定、低复杂度的蓝图来描述。我们强调的是神经生理学所教给我们的关于这个网络中计算和通信动力学的内容。我们的论题是大脑的计算单元(神经元和突触)可以表示为比较紧凑、具有一定功能性和表象的数学模型,而计算单元之间的通信则可以概括为异步的二进制消息(峰电位)。
我们所提方法的出发点主要是根据这样一个事实,即大脑的行为完全是通过个体功能单元之间非随机的以及相关联的互动而形成的,这也是有组织复杂性的一个关键特征。计算机建模与仿真往往要比封闭形式的分析和逐个分解更适合于这种复杂的系统。因此,在基于超级计算的模拟取得了长足进步的情况下,我们的方法的依据是我们坚信在适当抽象层次上进行大规模脑模拟意味着获得一个关键的科学工具,它将为测试有关计算的神经科学理论并发现认知的潜在机理提供机会。
对模拟的适当抽象层次做出判断是至关重要的。任何物理系统在建模时必须面对这个难题。如果我们选择过高的抽象层次,那么模型中的黑盒子本身会变得异常复杂,可能无法很好地随着我们理解能力的增长将其映射到现实中。反之,如果我们选择的抽象层次很低,工作层面的分辨率太高,则会耗费很多计算资源,并导致我们的理解力和注意力被分散到无关紧要的细节上。令人遗憾的是,没有任何捷径能使我们在一开始就找准抽象和分辨率之间的平衡。唯一的解决办法是以群体方式进行实验和探索。不同思想派别的涌现是有好处的 [13,14,16,25,38],其中每一派别都针对大脑概念化和模型化过程中所选的抽象层次持有各自的观点。已确立的传统大多是在相对较高的抽象层次上,包括在人工智能(AI)、认知科学、可视信息处理、连接主义、计算学习理论和贝叶斯信念网络等领域的尝试 [4,5,9,21-24,27,30,35,37]。同时,还有一部分尝试旨在确定与之相对的另一方面,即试图在模拟大脑组织的过程中获得不断提高层次的还原的生物学详细信息[20,36]。我们努力在这两种极端之间找到平衡 [11],并倡导一个中间路线[12,15,17]。与抽象的连接模型相比,这更偏向于神经科学,但与详尽的、准确的生物物理模拟相比,我们的模拟不那么深入细致。在不同的环境下,科学家武库中的望远镜、显微镜、双筒望远镜都有各自应有的位置。
神经解剖学
神经科学的核心原则(有时被称为“神经元学说”)假设大脑中特定的细胞,即神经元,是大脑计算的基本生物学单元。个体神经元的功能将在随后的神经生理学章节中阐述,但是在这里,我们把神经元的功能概括为获取、集成和发送二进制消息。这些消息在接触点被传递,英国的查尔斯·谢灵顿(Charles Sherrington)爵士在1897年将这种接触点命名为(神经元轴突的)突触。通过消息传递,神经元相互协作构成具有强大功能的网络,其处理能力比个体神经元的处理能力复杂、高级得多。为了理解大脑的功能,掌握神经回路的组织结构是至关重要的。
大脑中的连接是稀疏的。成年人有大约100万亿个突触,如果要对构成大脑的数十亿神经元进行完全和直接的连结,比全部直接连接几十亿神经元所需的突触数目少6个数量级。而且,有强有力的证据证实了生物针对组成这样的稀疏网络拥有相对紧凑的算法;与具有较适中的大脑和能力的动物(如啮齿类动物)相比,具有较大脑容量和较高的认知能力的动物(如猿猴)并没有相应的较大比例的基因组被用于执行神经性功能。也许不足为奇的是,神经解剖学家还没有找到一个与所有个体都不一样,异常错综复杂,由任意连接构成的网络。可以看到存在于个体大脑中的结构是大量重复的,各物种之间普遍存在同源性。
在所有哺乳动物大脑的表面是一层只有几毫米厚的组织,我们称之为大脑皮层,或简称为皮层。它被认为是更高级的认知所处的核心区域。其组织形态呈多尺度特性,皮层包括在水平运行的层次、垂直方向上集成的具有延伸深度的功能柱和由数百万柱体组成的大型的功能区域,最终形成由多个紧密连接的区域所构成的网络。在该系统中,神经元通过灰质实现局部连接,与此同时,通过远距离的白质连接,皮层能将信号传递到远端的皮层区域或皮层下目标(见图1和2)。
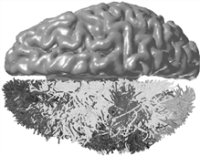
图1 使用我们算法创建的一个人脑白质束子集的俯视图
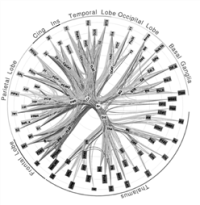
图2 一个由102个有组织层次的超区域和1 138个连接组成的猕猴大脑白质图。染色的长方形代表节点,染色的曲线代表边。白质发射束延伸到大脑的各个部位
最早的发现之一认为皮层结构包括了6个跨越皮层厚度的不同水平层面。已经找到一个由皮层之间和皮层内的连接所组成的特殊网络并对其进行了研究 [6],得出了各层之间活动传播的特征模式。为便于模拟,我们将这种典型的分层皮质-丘脑结构转化为原型灰质网络(参见图3)。
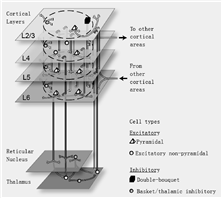
Cortical Layers 皮质层
Reticular Nucleus 网状核
Thalamus 丘脑
To other cortical areas 到其他的皮质区域
From other cortical areas 从其他的皮质区域
Cell types 细胞类型
Excitatory 兴奋性
Pyramidal 椎体的
Excitatory non-pyramidal 兴奋性非椎体的
Inhibitory 抑制性
Double-bouquet 双束
Basket/thalamic inhibitory 篮/丘脑抑制
图3 基于C2模拟器的皮质系统模拟回路示意图
各层之间的连接主要是垂直方向的,只有少量的横向传播,这些直径只有数十或数百微米的柱型结构称为“皮层功能柱”。在很多皮层区域,已经证实了位于相同功能柱中的神经元共同拥有相关的功能特性,这表明柱体不仅仅是结构性的实体,而且具有功能性[6,29]。在柱体范围内经过测量收集到的信息有助于我们构建大规模的脑模型,如图3所示。
皮层功能柱所占据的皮层区域通常只有几毫米的范围,看上去应该是负责特定的功能,包括运动神经的控制、视力和规划。著名的布罗德曼(Brodmann)脑区图《大脑皮层中的定位》,根据6个皮层中细胞密度的变化将大脑划分为皮层区域,从而表明了每个功能对应特定皮层回路的可能性[18]。例如,布罗德曼区域17被明确地关联到核心视觉处理功能。在数十年的时间里,有数百位科学家的工作主要集中在理解大脑中每个皮层区域如何发挥相应的功能,以及这些区域的解剖和连接结构是如何实现功能。
20世纪出现了压倒性的证据来支持皮层分区域与特定功能联系的观点,大脑也证明了结构可塑性的惊人程度。例如,目前已经证明了这样一个事实,在白鼬大脑发育的过程中,将白质中视觉通路连接到听觉皮层,同时将听觉通路连接到视觉皮层,通常被特化为对应听觉的区域也可以像被特化为对应视觉的区域一样起作用,反之亦然。这种令人吃惊的自然重构使我们可以期望神经计算的核心算法可能不依赖具体感觉器官或运动神经的形态,而观察到的各区域间的皮层结构变化可能表示典型神经回路的精细化。正是这些典型回路是我们期望进行逆向工程的对象。这种典型微回路的存在是一个重要假设[29],尽管大量的局部皮层线路布局已被测算出[6],但是,微回路的精确形式仍然是未知的,而且它在神经计算中所起的作用仍未得到证实。即使能够发现一个基础典型的回路,为了解开其潜在机理,我们仍必须找出并实现伴随的可塑性机制,这种机制保证了在发育成长和成熟阶段学习过程中实现典型回路的剪裁、精化和制定,以完成其特定功能。我们在后面会进一步探讨可塑性问题,特别是其可能的局部突触机制。
在神经系统组织结构最粗粒度规模上,多个皮层区域形成网络,以处理复杂的功能。例如,在阅读时,大脑执行一系列错综复杂的灵巧的眼睛运动,在字里行间进行扫描和定位以选取出一系列的线条和边缘组合(字母)来构成复杂的时空模式。这些模式可看作是用来开启一部语言学知识巨著的钥匙,这部巨著使大脑沐浴在对应词语含义的景象、声音、气味和物体特征中。令人惊讶的是,这复杂的功能特性是依靠一个小型的大脑区域网络来调节的,其中的各个区域在结构上彼此紧密连接而在空间上又存在一定距离。这使我们想到各种不同的脑功能可能是由分布在整个大脑之中的特征子网支撑,这些子网推动着信息的流动、集成,同时推动功能上存在差异的、分布的中心之间的合作。我们在IBM公司阿尔马登(Almaden)研究中心的研究组于2009年和2010年针对猕猴和人类大脑的白质结构的测量和分析过程,取得了两个重要的突破[28,32],可作为我们进一步理解大脑区域网络的一条途径(请参阅本文所附题为“猕猴大脑白质通路的分析”和“人类大脑白质通路的测量”的两个解说栏)。
神经生理学
生物细胞成为一个能够接收和集成输入,基于输入进行决策,并根据决策结果向其他细胞发送信号的结构,这是进化过程中的一个惊人成就。诺贝尔奖获得者圣地亚哥·拉蒙·卡哈尔(Santiago Ramon y Cajal)在1891年提出,这些细胞(即神经元)是大脑中信息处理和认知功能的基础。神经功能产生于神经元的3个主要结构性组件:树突,接收和集成输入的树状结构;神经元胞体,根据这些输入进行决策的地方;轴突,向近处和远处的神经元传送信号的修长、狭窄的结构。令人深刻印象的是,尽管细胞通常是微小的,但轴突能增长到比1米还长。
神经元内信号集成和传输的根本是神经元膜电位的波动,电压差跨在膜内外,膜将细胞内部和外部隔开。当离子经由选择性开启和关闭的通道穿过神经元膜时,这些电位波动就产生了。如果膜电位跨越临界阈值,神经元就会产生一个峰电位(即判定其接收到了值得注意的输入),这是一个沿着其轴突传送的可靠且形式固定的电化学信号。峰电位是大脑中重要信息的传递者,既可用作在视网膜的视神经中传递光的感知信号,也可在运动皮层经脊髓传递控制信号,来驱动相关肌肉,同时还可用于介于这两者之间的几乎每个步骤。
当一个峰电位到达其轴突的末端,信号的性质会发生变化。突触是连接一个神经元的轴突和另一个神经元的树突的微型结构,它将一个峰电位的电信号转换为化学信号,而后再重新将化学信号转换为电信号。峰电位神经元(在这个排列结构中被称为“突触前神经元”)释放一种被称为突触神经传递物的化学物质,这些物质可以迅速传播到其它神经元(称之为“突触后神经元”)。神经传递物将引发突触后细胞表面的离子通道的开启及随后接收方树突的膜电位的修改。这些变化既可以是刺激性的,意味着它们将使目标神经元被激发的可能性变大,也可以是抑制性的,使得它们的目标被激发的可能性变小。接收到的输入峰电位模式和神经元类型共同决定接收方神经元的最终峰电位模式。经过这个过程,某一神经元所发出峰电位的基本数字电信号,首先转换成能在各神经元之间传播的化学信号,然后再转换为能被接收方神经元集成的模拟电信号。
模拟的后突触兴奋程度称为“突触强度”,它在一个器官的生命期内是不确定的。因此,某一神经元对另一神经元的影响是可以改变的,也就改变神经元网络中的功能关系。加拿大心理学家唐纳德·赫布(Donald O. Hebb)提出了关于突触可塑性的著名推测,即“那些共同激发的神经元将会连接在一起”,也就是说,如果神经元A和B通常是在大致相同的时间激发峰电位,那么它们之间的突触强度会增加。作为当代对赫布观点的改进,研究者认为通过一种叫做“峰电位时间相关的突触可塑性(STDP)”的机制[33],突触强度可以根据突触前和突触后峰电位的时间相关性而改变。因此,如果神经元A恰好在神经元B激发前激发,那么神经元A将加强其到神经元B的连接;如果激发顺序是相反的,则连接强度会减弱。目前,还有一些正在进行中的研究工作,将神经调节类的化学制品,如多巴胺,与更加复杂的模仿强化学习更新规则的突触可塑性机制联系起来[31,34]。虽然突触可塑性机制是一个活跃的研究热点,但目前关于哪种机制是最普遍的或最重要的尚无定论。尽管如此,大脑研究者们普遍认为突触强度的变化是学习和记忆的基础,因此理解突触可塑性将为深入理解认知功能提供重要帮助。
以上描述提供了一个神经元行为的大致轮廓。神经学家们揭示了神经元功能更为详尽的情况,包括:产生膜电位振荡变化和调节激发模式的许多不同的离子通道,在一定时间变化范围操作的不同突触类型,引起神经元行为变化的神经调质,以及很多影响神经元功能的其他特征 [18]。基于这些特征,可以区分出很多不同的神经元类型,而且这些类型已在一些模型中捕捉到了。
值得注意的是,虽然普遍认为峰电位是大脑主要信息的传递者,但关于峰电位对信息如何进行编码仍存在相当多的争论。居于主导地位的观点认为脑皮层神经元利用其瞬时的激发频率对信息进行编码,而与峰电位之间的相对时间在本质上是无关的。尽管依赖峰电位频率的信息共享是有效的,然而有研究显示峰电位的精确定时有另外的价值。最新证据表明大脑能够探测并利用人为引入的精确峰电位定时。
我们认为,由于峰电位是神经通讯中的通用载体,一个重现大脑峰电位时序模式的模拟网络必然可以对神经计算进行充分模拟。在一个理想化的思维实验中,模拟过程将对整个大脑中峰电位的精确时序模式进行预测(包括神经元簇放电、神经元之间的相互关联以及时间同步),以应对任意刺激和语境定位。毫无疑问,这样的一个成就,如果可能实现,将意味着囊括了整个生物学神经计算。然而,引发很多研究者异议的是:认为这个成就意味着峰电位是研究和模拟神经系统的正确抽象层次。一方面,那些相信应选择在更高抽象层次上开展研究的人认为,这样的峰电位模拟细节与认知基本原则无关,而且实际上会掩盖基于大脑计算的关键算法[27];另一方面,那些相信有必要在更高分辨率层面上开展研究的人坚持认为,如果未将树突各部分详细动态、离子浓度和蛋白质构成引入到模拟过程中,峰电位序列的精确重构,即便是必要的,也很难实现。尽管如此,几乎没有大脑研究者对神经元是计算的基本细胞单位,峰电位是它们之间传递的信息这个观点有分歧。因此,峰电位构成了描述神经通讯的首选层面,所以我们将主要致力于研究与峰电位直接相关的模拟过程[2,3,15]。
超级计算模拟
神经解剖学(neuroanatomy)和神经生理学(neurophysiology)已经共同构建了一组丰富的针对大脑结构和动力学的约束条件。在自己的工作中,我们旨在将这些约束的一个经过审慎选择的子集整合并实施到单一的计算平台,也就是哺乳动物的大脑模拟器之上。
模拟器的基本要素包括:用于展示大量行为方式的表象模型神经元、峰电位通信、动态突触通道、可塑突触、结构可塑性,以及由分层、微功能柱、超功能柱、皮层区域和多区域网络组成的多尺度网络体系结构(如图3所示)。其中,每个要素都是模块化的并且可以单独配置,因此我们能够灵活地测试大量关于大脑结构和动力学的生物启发性假说。与之相应,其可能组合构成了极大的空间,这就要求模拟以一定的速率运行,从而能够实现迅速的、用户驱动的探索。
神经模拟的发展历史可以追溯到20世纪50年代。从那时开始,关于皮层模拟的研究(如图3所示)已经沿着两条路线发展:细节化和规模化。几个公开可用的模拟器,包括NEURON和GENESIS,适用于少量神经元的详细模拟[7]。但令人遗憾的是,引入这样精细的生物物理学细节会导致哺乳动物规模的近实时模拟任务在计算上无法实现。另一方面,其他研究工作已经利用紧凑的、显象的神经元,展示了对数百万神经元和几十亿突触的模拟。我们的目标 [3,15]是在获得近实时模拟速度的同时,沿着模型规模化和神经解剖学细节化的方向拓展尖端研究领域的边界。
在一个模拟平台之上同时达到的规模、速度和细节方面的要求,对于计算系统的三大资源——存储、计算和通信而言,是一项严峻的挑战。例如,猫的大脑皮层有将近10亿神经元以及超过6万亿个突触(如表1所示)。由于突触数量是神经元数量的1万倍以上,所需内存必须支持与突触数量成正比的模拟规模要求的状态表示数量。因此,即使我们能用一个字节的存储空间来描述一个突触的状态,一次猫科规模的模拟将至少需要6 TB的内存空间;每个突触的高效突触数据结构则需要大约16 B的存储空间。此外,假定每个神经元每毫秒更新一次,描述神经元状态演化的动态差分方程每秒必须计算1万亿次。采用生物学上认可的每秒1次的神经元激发的平均速率,大多数突触每秒就会接收到1次峰电位,因此将会有6万亿个峰电位消息在神经网络中传递。为了满足这一需求,我们将加快超级计算发展及算法和软件体系结构关键性创新的步伐。
表1 下列哺乳动物的神经元和突触
|
小鼠(Mouse) |
大鼠(Rat) |
猫(Cat) |
猴子(Monkey) |
人(Human) |
|
|
十亿神经元(Billions of Neurons) |
0.016 |
0.055 |
0.763 |
2 |
20 |
|
万亿突触(Trillions of Synapses) |
0.128 |
0.442 |
6.10 |
16 |
200 |
从硬件方面来说,蓝色基因超级计算机系统提供了众多的计算处理器、大量的分布式内存以及低延迟、高带宽的通信子系统。从软件方面来说,我们已经开发了一个称为C2的脑皮层模拟器,该模拟器采用了分布式存储多处理器的体系结构。我们模拟的规模持续扩大,引入到我们的模拟中的神经生理学和神经解剖学约束不断增加(参见题为《脑皮层模拟器设计和实施》的附加说明)。
2007年以来,从针对小鼠和大鼠[3]脑皮层规模的早期工作开始,我们的模拟在规模方面一直保持稳步增长。2009年5月,在与劳伦斯伯克利(Lawrence Berkeley)国家实验室的合作中,我们使用“黎明”(Dawn Blue Gene/P)蓝色基因超级计算机系统,获得了最新的研究结果(如图4所示)。该研究成果充分利用了超级计算机系统的存储能力,是具有新闻价值的猫科-规模脑皮层模拟(大致相当于人脑规模的4.5%)的里程碑[2]。这些模拟网络展示了神经元通过自组织形成可重现且具有锁时特性的非同步分组 [3]。模拟还以α(8~12 Hz)和γ(>30 Hz)的频率,重现了在哺乳动物脑皮层大片区域中经常出现的神经活动层次的振荡。在一个类似视觉刺激的范式中,模拟网络显示出的特定种群相关的反应延迟是与在哺乳动物脑皮层中所观察到的一致 [2]。模拟器的一个重要优势是使我们能够分析数十万个神经组织,而动物记忆是有限的,同时仅能记录数十个神经群体。利用该优势,我们可以构造出刺激-诱发活动在网络中传播的详细图景;图5概括了以下活动,从丘脑传递到大脑皮层的第4和6层,然后再传递到第2、3和5层,同时在各层内横向传播。
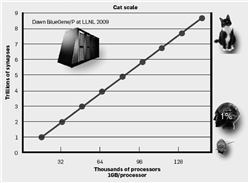
图4 利用C2的可伸缩脑皮层模拟
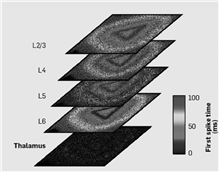
图5 针对一个三角形刺激丘脑回路的模拟反应
C2模拟器为发现大脑中的算法提供了一个关键的综合工作台。虽然到目前为止,我们的模拟包括了很多神经结构和动力学的关键特征,但还仅是触及到现有神经科学数据的表面。例如,我们正在引入长距白质投射(参见前两个附加解说栏及图1和图2),其它重要皮层下结构(如基底神经节)以及结构可塑性机制。我们始终以开放的态度来应对新兴技术带来的详细皮层回路的全新测量方法。
期望认知功能可以从这些在神经生物学启发下实现的模拟中自发产生是不现实的。我们的期望是模拟器可提供一个与大脑一致的基底,据此我们可以形成和表现神经计算理论。通过研究模拟的行为,我们希望能够为心智从大脑中产生的完整数学理论解释提供一些线索,以期用于开发智能商用机器。就这一点而言,我们所构建的模拟结构并不是答案而只是用于发现的工具,如同线性加速器(之用于探索物质结构)一样,它将为未来深入理解脑计算和实现神经形态工程创新奠定基础。
展望
对智能机器的探索最终需要在哲学、神经解剖学、神经生理学、计算神经科学,超级计算和计算机体系结构等领域有新的突破,并将这些新突破连贯、统一地结合在一起,以应对前所未有的挑战。认知计算领域的发展现状可以用温斯顿·丘吉尔(Winston Churchill)的话作最好的概括:“现在并不是终结。终结甚至还没有开始。但是现在可能是序幕的结束。”
随着模拟规模的急剧扩大和巨型计算机技术的不断发展,带来的好消息是,在十年的时间内,对人类规模的脑皮层的模拟不仅会成为现实,而且似乎不可避免。
同时,坏消息是,这样的模拟过程所要求的能源和空间要比生物大脑所要求的大好几个数量级。这种差异的根源应当归结为冯·诺依曼体系结构和大脑本身之间的显著差别[39]。现代计算假定存在一个存储程序模型,该模型通常是由数字、同步、串行、集中、快速、固定连线、通用和脆弱的电路来实现,并使用显式存储地址,在计算和数据之间有明确的划分。与之形成鲜明对比的是,大脑使用可再生的计算单元,即神经元和突触,利用混合模式的模拟-数字、异步、并行、分布式、缓慢、可重构、专门和容错的生物基质来实现,利用隐式的存储地址来弱化计算和数据之间的界限。
生物的优雅和效率引发我们探索全新的计算体系、系统设计和编程范例。美国国防高级研究计划局从2008年开始了“神经形态自适应可塑可伸缩电子系统”项目。在此项目的支持下,我们正在进行着一个雄心勃勃的计划。该计划的目标是通过寻求纳米技术和神经形态的超大规模集成技术突破,生成一个革命性的紧密型、低功率的神经形态芯片,其中每平方厘米包含100万神经元和100亿突触[26]。
最后,令人不快的消息是大脑中实现的核心算法集迄今仍未被发现,这使得我们的研究工作在拥有许多机遇的同时也充满了不确定性。为了应对这一挑战,需要一个拥有足够资源的交叉学科研究团体付出坚持不懈的努力[1]。目前,这个大努力正在以“多尺度”研究的方式并行推进:抽象认知原语和人工神经网络、极其详尽的生物学模型以及我们和其他研究者所支持的峰电位通讯基本语言。我们希望未来的发现将证明这些方法是互补的。其中,每种方法都拥有自身的优势,并且都对认知计算挑战的统一的解决作出贡献。我们在此引用美国能源部长和诺贝尔奖获得者朱棣文(Steven Chu)的具有启发性和充满激情的话语:“我不会低估应对这些挑战的难度,但我仍乐观地认为我们能够面对这些挑战。我相信我们国家和经济的活力,同时作为一个科学家,我一直乐观地认为我们有能力拓展我们能力的疆界。”
致谢
本研究报告受到(美国)国防高级研究计划局国防科学办公室的“神经性自适应可塑可微缩电子系统(SyNAPSE)”项目的资助(合同号为HR0011-09-C-0002)。其中的见解和结论仅代表几位作者的个人观点,而不应理解为代表(美国)国防高级研究计划局或美国的政府明确或隐含的官方意见。
感谢霍斯特·西蒙(Horst Simon)的合作,也感谢美国能源部国家核安全管理局的先进模拟和计算计划在劳伦斯利弗莫尔(Lawrence Livermore)国家实验室的蓝色基因超级计算机项目上所倾注的时间,该项目(合同号为DE-AC5207NA27344)是由劳伦斯利弗莫尔国家安全有限责任公司负责实施的。我们同时也大大受益于IBM公司的阿尔马登研究中心和托马斯沃特森(Thomas J. Watson)研究中心的超级计算资源以及KAUST/IBM中心的深度计算研究。
衷心感谢宾泽格(T. Binzegger)、道格拉斯(R. J. Douglas)和马丁(K. A. C. Martin)让我们共享了他们的丘脑皮层连接性数据。同时,由于与格雷戈里·科拉多(Gregory Corrado)一起所做的大量深入的探讨,使得我们的阐释变得更加清晰明了。
作者: 哈门德拉·莫德哈(Dharmendra S. Modha)
拉加科帕勒·安安塔纳拉雅楠(Rajagopal Ananthanarayanan)等
译者: 史忠植
译者致谢
本文翻译中,韩旭做了认真的修改,原执行主编冀复生做了认真的推敲和校对,提高了译文的准确性和可读性。在此表示感谢。
作者:
哈门德拉·莫德哈(Dharmendra S. Modha),IBM阿尔马登研究中心认知计算主管。
拉加科帕勒·安安塔纳拉雅楠(Rajagopal Ananthanarayanan),谷歌技术组成员,在IBM阿尔马登研究中心任职期间参与此项工作。
史提芬·埃瑟尔(Steven K. Esser),IBM阿尔马登研究中心研究人员。
安东尼·尼迪兰格(Anthony Ndirango),在IBM阿尔马登研究中心任职期间参与此项工作。
安东尼·谢邦狄(Anthony J. Sherbondy),在IBM阿尔马登研究中心任职期间参与此项工作。
拉哈文达·辛格(Raghavendra Singh),IBM印度研究中心研究人员。
译者:
史忠植:CCF会士。中国科学院计算技术研究所研究员。主要研究方向为智能科学。E-mail:shizz@ics.ict.ac.cn
参考文献:
[1] Albus, J.S., Bekey, G.A., Holland, J.H., Kanwisher, N.G.,Krichmar, J.L., Mishkin, M., Modha, D.S., Raichle, M.E.,Shepherd, G.M., and Tononi, G. A proposal for a decade of the Mind Initiative [Letter]. Science 317, 5843 (Sept. 7, 2007), 1321.
[2] Ananthanarayanan, R., Esser S.K., Simon H.D.,and Modha, D.S. The cat is out of the bag: Cortical simulations with 109 neurons and 1013 synapses. Gordon Bell Prize Winner. In Proceedings of the ACM/IEEE Conference on Supercomputing (Portland, OR,Nov. 14-20). ACM , New York, NY, 2009, 1-12.
[3] Ananthanarayanan, R. and Modha, D.S. Anatomy of a cortical simulator. In Proceedings of the ACM/IEEE Conference on Supercomputing (Reno, NV, Nov.10-26). ACM , New York, NY, 2007, 3-14.
[4] Arbib, M., Ed. The Handbook of Brain Theory and Neural Networks. MIT Press, Cambridge, MA, 2002.
[5] Baumgartner, P. and Payr, S. Eds. Speaking Minds: Interviews with 20 Eminent Cognitive Scientists. Princeton University Press, Princeton, NJ, 1995.
[6] Binzegger, T., Douglas, R.J., and Martin, K.A.A. Quantitative map of the circuit of cat primary visual cortex. Journal of Neuroscience 24, 39 (Sept. 2004), 8441-8453.
[7] Brette, R. et al. Simulation of networks of spiking neurons: A review of tools and strategies. Journal of Computational Neuroscience 23, 3 (July, 2007), 349-398.
[8] Gazzaniga, M.S. The Cognitive Neurosciences, Fourth Edition. MIT Press, Cambridge, MA, 2009.
[9] George, D. and Hawkins, J. Towards a mathematical theory of cortical microcircuits. PLoS Computational Biology 5, 10 (Oct. 2009), e1000532.
[10] Goertzel, B. and Pennachin, C. Artificial General Intelligence. Springer, Berlin, Heidelberg, 2009.
[11] Herz, A.V.M., Gollisch, T., Machens, C.K., and Jaeger, D. Modeling single-neuron dynamics and computations: A balance of detail and abstraction. Science 314, 5796 (Oct. 2006), 80.
[12] Hill, S. and Tononi, G. Modeling sleep and wakefulness in the thalamocortical system. Journal of Neurophysiology 93, 3 (Nov. 2005), 1671-1698.
[13] Hodgkin, A.L. and Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. Journal of Physiology 117, 4 (Aug. 1952), 500-544.
[14] IEEE Symposium on Information Theory. MIT, Cambridge, MA, 1956.
[15] Izhikevich, E.M. and Edelman, G.M. Large-scale model of mammalian thalamocortical systems. Proceedings of the National Academy of Sciences of the USA 105, 9 (Mar. 2008), 3593-3598.
[16] Jeffress, L.A. Cerebral Mechanisms in Behavior: The Hixon Symposium. John Wiley & Sons, Inc., New York, 1955.
[17] Johansson, C. and Lansner, A. Towards cortex-sized artificial neural systems. Neural Networks 20, 1 (Jan. 2007), 48-61.
[18] Kandel, E.R., Schwartz, J.H., and Jessell, T.M. Principles of Neural Science, Fourth Edition. McGraw-Hill Medical, New York, 2000.
[19] K?tter, R. Online retrieval, processing, and visualization of primate connectivity data from the CoCoMac database. Neuroinformatics 2, 2 (June 2004), 127-144.
[20] Markram, H. The Blue Brain Project. National Review of Neuroscience 7, 2 (Feb. 2006), 153-160.
[21] Marr, D. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information. W.H. Freeman, Cambridge, MA, 1983.
[22] McCarthy, J. Generality in artificial intelligence. In Formalizing Common Sense, V. Lifschitz, Ed. Ablex,Bristol, U.K., 1990, 226-236.
[23] McClelland, J.L. and Rumelhart, D.E. Parallel Distributed Processing. In Psychological and Biological Models, Volume 2. MIT Press, Cambridge, MA, 1987.
[24] McCulloch, W.S. and Pitts, W. How we know universals: The perception of auditory and visual forms. Bulletin of Mathematical Biology 9, 3 (Sept. 1947), 127-147.
[25] McCulloch, W.S. and Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biophysics 5 (1943), 115-133.
[26] Mead, C. Analog VLSI and Neural Systems. Addison Wesley Publishing Co., Boston, 1989.
[27] Minsky, M. The Emotion Machine: Commonsense Thinking, Artificial Intelligence, and the Future of the Human Mind. Simon & Schuster, New York, 2006.
[28] Modha, D.S. and Singh, R. Network architecture of the long-distance pathways in the macaque brain. Proceedings of the National Academy of Sciences of the USA 107, 30 (June 2010), 13485-13490.
[29] Mountcastle, V.B. Perceptual Neuroscience: The Cerebral Cortex. Harvard University Press, Cambridge, MA, 1998.
[30] Rosenblatt, F. The Perceptron: A probabilistic model for information storage and organization in the brain. Psychological Review 65, 6 (Nov. 1958), 386-408.
[31] Schultz, W., Dayan, P., and Montague, P.R. A neural substrate of prediction and reward. Science 275, 5306 (Mar. 1997), 1593-1599.
[32] Sherbondy, A.J., Dougherty, RF., Ananthanaraynan, R., Modha, D.S., and Wandell, B.A. Think global, act local: Projectome estimation with BlueMatter. In Proceedings of the Medical Image Computing and Computer Assisted Intervention Society, Lecture Notes in Computer Science (London, Sept. 20-24). Springer, Berlin, 2009, 861-868.
[33] Song, S., Miller, K.D., and Abbott, L.F. Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nature Neuroscience 3, 9 (Sept. 2000), 919-926.
[34] Sutton, R.S. and Barto, A.G. Toward a modern theory of adaptive networks: Expectation and prediction. Psychological Review 88, 2 (Mar. 1981), 135-140.
[35] Teddington Symposium on the Mechanization of Thought Processes (National Physical Laboratory, Nov. 24-27). Her Majesty’s Stationary Office, London, 1958.
[36] Traub, R.D., Contreras, D., Cunningham, M., Murray, H., LeBeau, F.E.N., Roopun, A., Bibbig, A., Wilent, W.B., Higley, M., and Whittington, M.A. Single-column thalamocortical network model exhibiting gamma oscillations, spindles, and epileptogenic bursts. Journal of Neurophysiology 93, 4 (Nov. 2005), 2194-2232.
[37] Valiant, L.G. Circuits of the Mind. Oxford University Press, New York, 2000.
[38] von Hayek, F.A. The Sensory Order: An Inquiry Into the Foundations of Theoretical Psychology. University of Chicago Press, Chicago, 1952.
[39] von Neumann, J. The Computer and the Brain, Second Edition. Yale University Press, New Haven, CT, 2000.